对称密钥的缺点
我们先看一个例子,小明和小红要进行通信,但是不想被其他人知道通信的内容,所以双方决定采用对称加密的方式。他们做了下面的事情:
1、双方商定了加密和解密的算法
2、双方确定密钥
3、通信过程中采用这个密钥进行加密和解密
这是不是一个看似完美的方案?但其中有一个步骤存在漏洞!
问题出在步骤2:双方确定密钥!
你肯定会问,双方不确定密钥,后面的加、解密怎么做?
问题在于确定下来的密钥如何让双方都知道。密钥在传递过程中也是可能被盗取的!这里引出了一个经典问题:密钥配送问题。
密钥配送问题
小明和小红在商定密钥的过程中肯定会多次沟通密钥是什么。即使单方一次确定下来,也要发给对方。加密是为了保证信息传输的安全,但密钥本身也是信息,密钥的传输安全又该如何保证呢?难不成还要为密钥的传输再做一次加密?这样不就陷入了死循环?
你是不是在想,密钥即使被盗取,不还有加密算法保证信息安全吗?如果你真的有这个想法,那么赶紧复习一下上一篇文章讲的杜绝隐蔽式安全性。任何算法最终都会被破译,所以不能依赖算法的复杂度来保证安全。
小明和小红现在左右为难,想加密就要给对方发密钥,但发密钥又不能保证密钥的安全。他们应该怎么办呢?
有如下几种解决密钥配送问题的方案:
- 事先共享密钥
- 密钥分配中心
- Diffie-Hellman密钥交换
- 非对称加密
本文就不展开讲每种方式,这里只是为了引出今天的主角——非对称加密。
非对称加密
非对称加密也称为公钥密码。我更愿意用非对称加密这种叫法。因为可以体现出加密和解密使用不同的密钥。
对称加密中,我们只需要一个密钥,通信双方同时持有。而非对称加密需要4个密钥。通信双方各自准备一对公钥和私钥。其中公钥是公开的,由信息接受方提供给信息发送方。公钥用来对信息加密。私钥由信息接受方保留,用来解密。既然公钥是公开的,就不存在保密问题。也就是说非对称加密完全不存在密钥配送问题!你看,是不是完美解决了密钥配送问题?
回到刚才的例子,小明和下红经过研究发现非对称加密能解决他们通信的安全问题,于是做了下面的事情:
1、小明确定了自己的私钥 mPrivateKey,公钥 mPublicKey。自己保留私钥,将公钥mPublicKey发给了小红
2、小红确定了自己的私钥 hPrivateKey,公钥 hPublicKey。自己保留私钥,将公钥 hPublicKey 发给了小明
3、小明发送信息 “周六早10点soho T1楼下见”,并且用小红的公钥 hPublicKey 进行加密。
4、小红收到信息后用自己的私钥 hPrivateKey 进行解密。然后回复 “收到,不要迟到” 并用小明的公钥mPublicKey加密。
5、小明收到信息后用自己的私钥 mPrivateKey 进行解密。读取信息后心里暗想:还提醒我不迟到?每次迟到的都是你吧?
以上过程是一次完整的request和response。通过这个例子我们梳理出一次信息传输的非对称加、解密过程:
1、消息接收方准备好公钥和私钥
2、私钥接收方自己留存、公钥发布给消息发送方
3、消息发送方使用接收方公钥对消息进行加密
4、消息接收方用自己的私钥对消息解密
公钥只能用做数据加密。公钥加密的数据,只能用对应的私钥才能解密。这是非对称加密的核心概念。
下面我用一个更为形象的例子来帮助大家理解。
我有下图这样一个信箱。
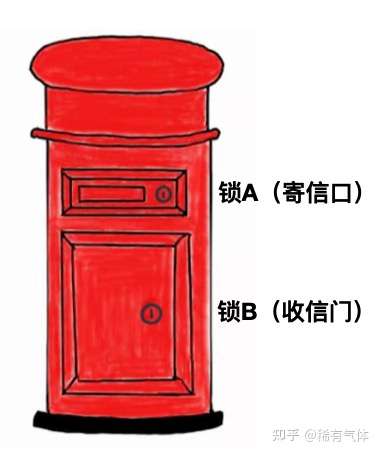
由于我只想接收我期望与之通信的朋友信件。于是我在投递口加了一把锁,这把锁的钥匙(公钥)我可以复制n份,发给我想接受其信件的人。只有这些人可以用这把钥匙打开寄信口,把信件投入。
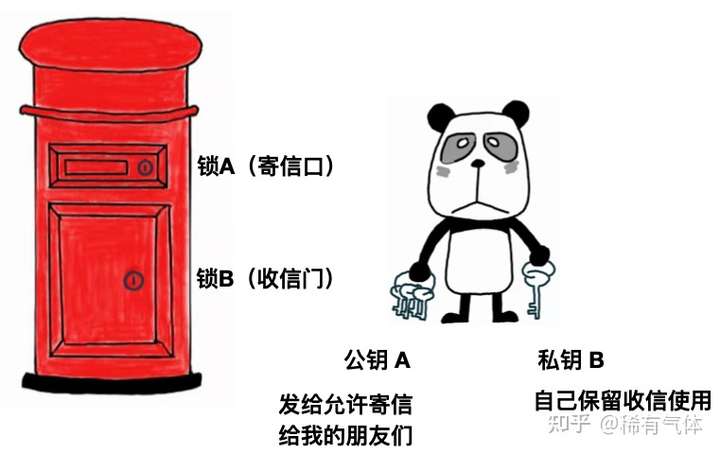
收信门是另外一把锁,打开后可以拿出所有的信件。寄信口的钥匙并不能打开这把锁。这把锁的钥匙(私钥)当然只有我有。我可以用这把钥匙打开信箱门,取出所有发给我的信件。
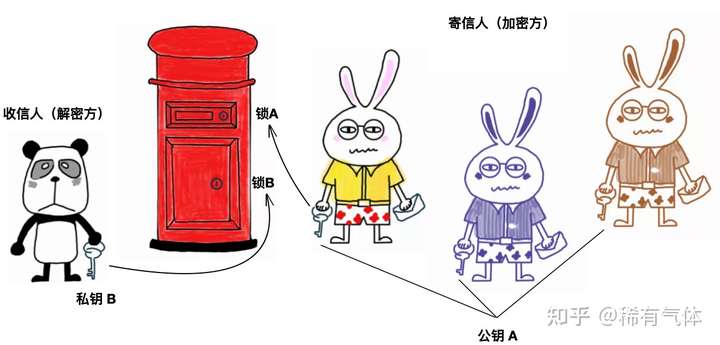
相信通过这个例子,可以帮助大家彻底理解公钥和私钥的概念。
非对称加密算法
RSA 是现在使用最为广泛的非对称加密算法,本节我们来简单介绍 RSA 加解密的过程。
RSA 加解密算法其实很简单:
密文=明文^E mod N
明文=密文^D mod N
RSA 算法并不会像对称加密一样,用玩魔方的方式来打乱原始信息。RSA 加、解密中使用了是同样的数 N。公钥是公开的,意味着 N 也是公开的。所以私钥也可以认为只是 D。
我们接下来看一看 N、E、D 是如何计算的。
1、求 N
首先需要准备两个很大质数 a 和 b。太小容易破解,太大计算成本太高。我们可以用 512 bit 的数字,安全性要求高的可以使用 1024,2048 bit。
N=a*b
2、求 L
L 只是生成密钥对过程中产生的数,并不参与加解密。L 是 (a-1) 和 (b-1) 的最小公倍数
3、求 E(公钥)
E 有两个限制:
1<E<
E和L的最大公约数为1
第一个条件限制了 E 的取值范围,第二个条件是为了保证有与 E 对应的解密时用到的 D。
4、求 D(私钥)
D 也有两个限制条件:
1<D<L
E*D mod L = 1
第二个条件确保密文解密时能够成功得到原来的明文。
由于原理涉及很多数学知识,这里就不展开细讲,我们只需要了解这个过程中用到这几个数字及公式。这是理解RSA 安全性的基础。
RSA的安全性
暴力破解私钥(D)
由于 N 在公钥中是公开的,那么只需要破解 D,就可以解密得到明文。
在实际使用场景中,质数 a,b 一般至少1024 bit,那么 N 的长度在 2048 bit 以上。D 的长度和 N 接近。以现在计算机的算力,暴力破解 D 是非常困难的。
通过公钥(E、N)计算出私钥(D)
公钥是公开的,也就是说 E 和 N 是公开的,那么是否可以通过 E 和 N 推断出 D 呢?
E*D mod L = 1
想要推算出 D 就需要先推算出 L。L 是 (a-1) 和 (b-1) 的最小公倍数。想知道 L 就需要知道质数 a 和 b。破解者并不知道这两个质数,想要破解也只能通过暴力破解。这和直接破解 D 的难度是一样的。
等等,N 是公开的,而 N = a*b。那么是否可以对 N 进行质因数分解求得 a 和 b 呢?好在人类还未发现高效进行质因数分解的方法,因此可以认为做质因数分解非常困难。
但是一旦某一天发现了快速做质因数分解的算法,那么 RSA 就不再安全
潜在的危险
我们可以看出大质数 a 和 b 在 RSA 算法中的重要性。保证 a 和 b 的安全也就确保了 RSA 算法的安全性。a 和 b 是通过伪随机生成器生成的。一旦伪随机数生成器的算法有问题,导致随机性很差或者可以被推断出来。那么 RSA 的安全性将被彻底破坏。
中间人攻击
中间人攻击指的是在通信双方的通道上,混入攻击者。他对接收方伪装成发送者,对放送放伪装成接收者。
他监听到双方发送公钥时,偷偷将消息篡改,发送自己的公钥给双方。然后自己则保存下来双方的公钥。
如此操作后,双方加密使用的都是攻击者的公钥,那么后面所有的通信,攻击者都可以在拦截后进行解密,并且篡改信息内容再用接收方公钥加密。而接收方拿到的将会是篡改后的信息。实际上,发送和接收方都是在和中间人通信。
要防范中间人,我们需要使用公钥证书。这部分内容在下一篇文章里会做介绍。
总结
和对称加密相比较,非对称加密有如下特点:
1、非对称加密解决了密码配送问题
2、非对称加密的处理速度只有对称加密的几百分之一。不适合对很长的消息做加密。
3、1024 bit 的 RSA不应该在被新的应用使用。至少要 2048 bit 的 RSA。
RSA 解决了密码配送问题,但是效率更低。所以有些时候,根据需求可能会配合使用对称和非对称加密,形成混合密码系统,各取所长。
最后提醒大家,RSA 还可以用于签名,但要注意是私钥签名,公钥验签。发信方用自己的私钥签名,收信方用对方公钥验签。